문제
https://leetcode.com/problems/majority-element/?envType=study-plan-v2&envId=top-interview-150
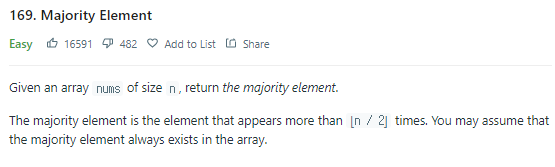
Example 1:
Input: nums = [3,2,3]
Output: 3Example 2:
Input: nums = [2,2,1,1,1,2,2]
Output: 2
✔ 문제접근 #1 해시테이블[통과] ⭕
Intuition
각 요소값이 등장하는 횟수를 해시테이블을 통하여 관리해준다.
Algorithm
배열을 순회하며 각 요소가 등장하는 횟수를 count라는 dict 자료구조에 기록해준다.초기값은 배열의 첫번째 값의 등장횟수 1을 최대라고 생각하고 시작한다.
등장 횟수를 기록해주면서 동시에 현재까지 가장 많이 등장한 횟수의 최댓값을 갱신해준다.
def majorityElement(self, nums: List[int]) -> int:
count = dict()
max_value_elem = nums[0] # 최대로 많이 등장한 key
max_value = 1 # 최대로 많이 등장한 key의 등장횟수
for elem in nums: #O(n)
if elem not in count:
count[elem] = 1
else:
count[elem] += 1
if max_value < count[elem]:
max_value = count[elem]
max_value_elem = elem
return max_value_elem
Complexity Analysis
- 시간 복잡도 : O(N)
- num 배열을 순차탐색 O(M)
- dict 자료구조의 in 연산 평균O(1)
- 그러므로 전체시작복잡도 : O(N)
- 공간복잡도 : O(N)
- 별도의 dict자료구조를 사용하였다. 평균O(N)
기타풀이 및 회고
기타 떠오르는 풀이로는 문제에서 과반수 이상의 수가 하나는 무조건 주어진다고 약속이 되어있기 때문에 배열을 정렬할 수 있다. 정렬하게 되면 과반수 이상이 되는 값은 무조건 배열의 맨 가운데는 거치게 되어있다. 그러므로 nums[n//2]의 값이 정답이 된다. 이와 같은 풀이의 경우 정렬하는데에 시간복잡도가 평균적으로 O(NlogN)이 소요 된다. 그러므로 좋은 방법은 아닌 것 같다.
다른 풀이로는 Moore Voting Algorithm이라는 풀이법이 있었다. 이 알고리즘은 배열에서 과반수가 넘는 데이터가 있는지 확인하고 찾을 때 사용하는 알고리즘이다.
후보의 등장 횟수 count와, 후보요소 condidate의 변수를 통해서, 요소를 순차적으로 탐색한다.현재 후보와 비교하여 서로 다르다면 후보 등장 횟수를 감소시키고, 서로 같다면 등장 횟수를 증가시킨다.만약 순차탐색 중 현재 후보 등장 횟수(count)가 0이라면 새로운 후보로 현재 들어온 값을 지정해주면 된다.이런 방식으로 진행하면 결국 과반수 이상이 되는 요소가 후보로 남게 된다.
def majorityElement(self, nums: List[int]) -> int:
count = 0
candidate = 0
for num in nums:
if count == 0:
candidate = num
if num == candidate:
count += 1
else:
count -= 1
return candidate시간복잡도는 선형탐색으로 O(N), 그리고 공간복잡도는 추가적인 자료구조를 사용하지 않기 때문에 O(1)의 공간복잡도를 가지게 된다.
'algorithm > 리트코드' 카테고리의 다른 글
| [리트코드] 150. Evaluate Reverse Polish Notation (0) | 2023.09.01 |
|---|---|
| [리트코드] 155. Min Stack (0) | 2023.09.01 |
| [리트코드] 80. Remove Duplicates from Sorted Array II (0) | 2023.08.31 |
| [리트코드] 26. Remove Duplicates from Sorted Array (0) | 2023.08.30 |
| [리트코드] 27. Remove Element (0) | 2023.08.30 |
