문제
https://leetcode.com/problems/find-peak-element/?envType=study-plan-v2&envId=top-interview-150
Example 1:
Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.Example 2:
Input: nums = [1,2,1,3,5,6,4]
Output: 5
Explanation: Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.Constraints:
- 1 <= nums.length <= 1000
- -2**31 <= nums[i] <= 2**31 - 1
- nums[i] != nums[i + 1] for all valid i.
✔ 문제접근 #1 완전탐색[통과] ⭕ -> 요구사항 만족❌
Intuition
배열 전체를 순회하며 peak값을 찾는다.
Algorithm
배열을 순회하며 양쪽값이 자신보다 작다면 peak로 판단하고 해당 index를 반환한다.
def findPeakElement(self, nums: List[int]) -> int:
# 배열의 요소가 1개일 경우는 그 값이 Peak
if len(nums) == 1:
return 0
INF = sys.maxsize
for i in range(len(nums)):
if i == 0:
if -INF < nums[i] and nums[i + 1] < nums[i]:
return i
if i == len(nums) - 1:
if nums[i - 1] < nums[i] and -INF < nums[i]:
return i
if nums[i - 1] < nums[i] and nums[i + 1] < nums[i]:
return i
Complexity Analysis
- 시간 복잡도 : O(N)
- num 배열을 순차탐색 O(N)
- 그러므로 전체시작복잡도 : O(N)
- 공간복잡도 : O(1)
✔ 문제접근 #2 이진탐색 [통과] ⭕ -> 요구사항 만족 ⭕
Intuition
배열하지 않아도 이진탐색을 통해 peak값을 찾을 수 있다.
요구사항의 log(N)에 문제를 해결할 수 있다.
Algorithm
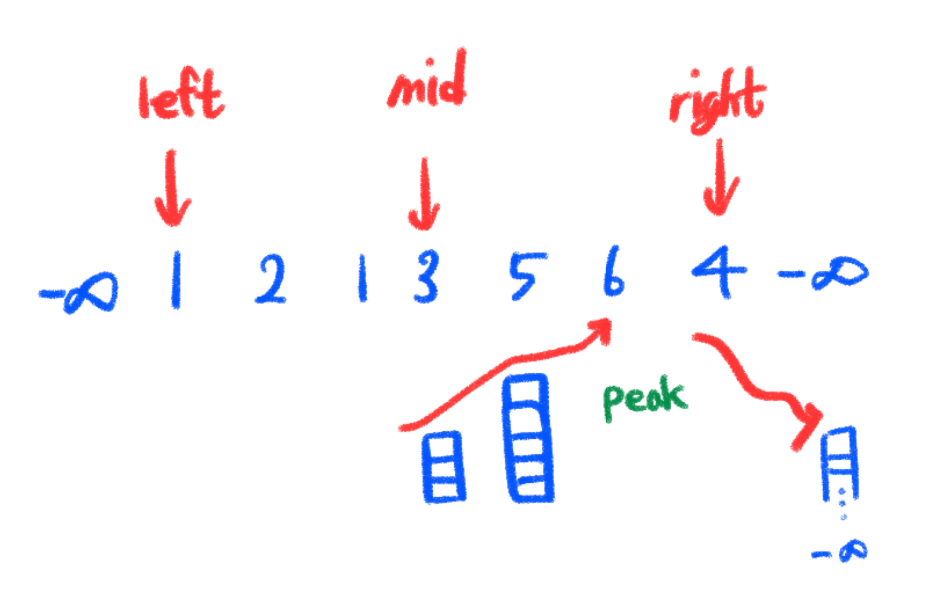
left, right 포인터를 통하여 mid를 구한다. 만약 mid에 해당하는 값보다 mid + 1이 더 크다면 반드시 [mid, num.length - 1] 구간 안에 peak값이 존재한다. 그 이유는 반드시 nums[mid] < nums[mid + 1] .... > -∞ 가 성립하므로 mid의 오른쪽 구간 중 최소 한개는 peak를 가지게 된다.
이진탐색시 mid, mid - 1, mid + 1의 인덱스에 주의해야 한다.
def findPeakElement(self, nums: List[int]) -> int:
INF = sys.maxsize
# 배열의 요소가 1개일 경우는 그 값이 Peak
if len(nums) == 1:
return 0
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
b = nums[mid]
if mid == len(nums) - 1:
a = nums[mid - 1]
c = -INF
elif mid == 0:
a = -INF
c = nums[mid + 1]
else:
a, c = nums[mid - 1], nums[mid + 1]
if b < c:
left = mid + 1
elif a > b:
right = mid - 1
else:
return mid
Complexity Analysis
- 시간 복잡도 : O(log(N))
- num 배열을 이진탐색 O(log(N))
- 그러므로 전체시작복잡도 : O(log(N))
- 공간복잡도 : O(1)
기타풀이 및 회고
이 문제는 num배열의 길이가 길지 않아서 선형탐색으로도 충분히 해결할 수 있지만, 요구사항에 log(N)의 시간복잡도로 해결이라는 점에서 많이 헤매었다. 사실 log(N)의 시간복잡도에 해결한다고 했을 때 바로 떠오르는 알고리즘은 이진탐색이었다. 그러나 해당문제에 이진탐색을 어떻게 적용시킬지에서는 정말 많이 헤매었다.
이진탐색의 경우 배열이 정렬된 상태에서 사용할 수 있다. 그렇다면 해당 배열을 정렬해도 될까?
배열을 정렬하는 순간 최소 Nlog(N)의 시간복잡도를 사용하기 때문에 요구사항을 만족할 수 없다.
그렇다면 정렬되지 않는 상태에서 바로 이진탐색을 사용하여 탐색했을 때 원하는 답을 구할 수 있을까? 두둥.. 이 문제는 해결할 수 있다가 정답이다.
단순히 "이진탐색은 반드시 정렬해야해! 라는 고정관념 때문에 많이 헤맨 것 같다. 원하는 요구사항에 맞는 값을 이진탐색으로 탐색할 수 있을까?를 충분히 고민해봐야 겠다.
'algorithm > 리트코드' 카테고리의 다른 글
| [리트코드] 125. Valid Palindrome (0) | 2023.09.10 |
|---|---|
| [리트코드] 530. Minimum Absolute Difference in BST (0) | 2023.09.08 |
| [리트코드] 55. Jump Game (0) | 2023.09.01 |
| [리트코드] 122. Best Time to Buy and Sell Stock II (0) | 2023.09.01 |
| [리트코드] 121. Best Time to Buy and Sell Stock (0) | 2023.09.01 |
